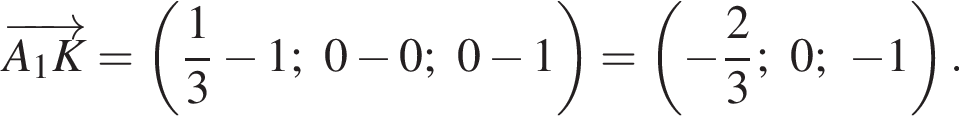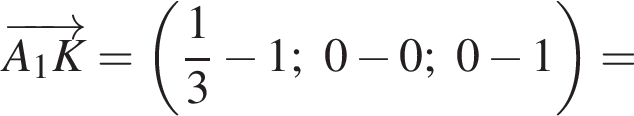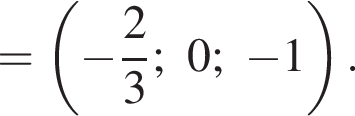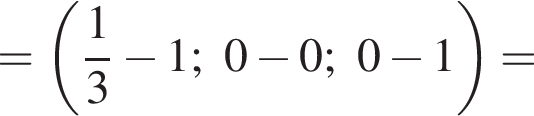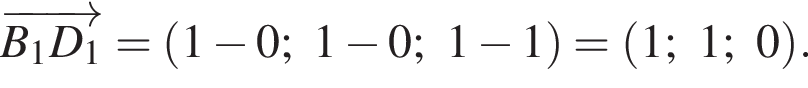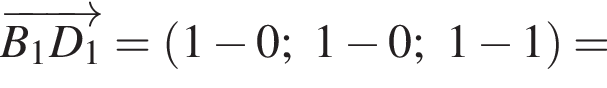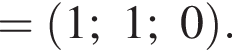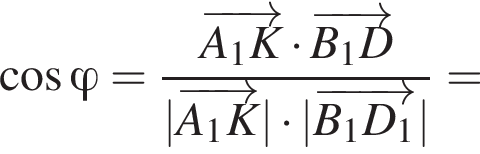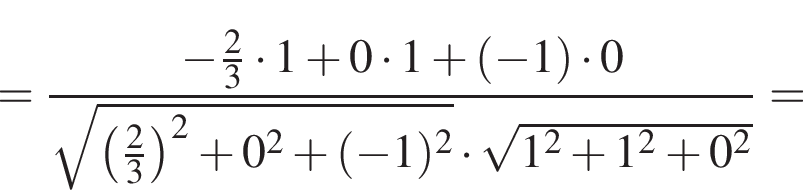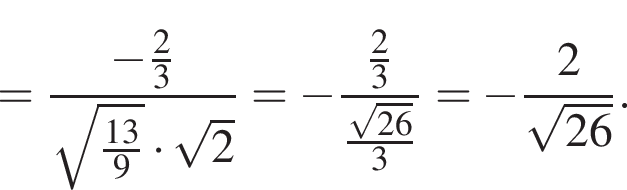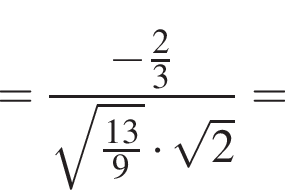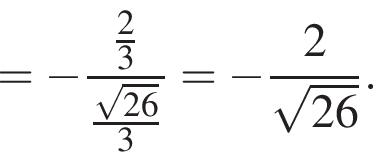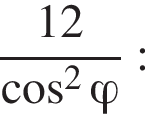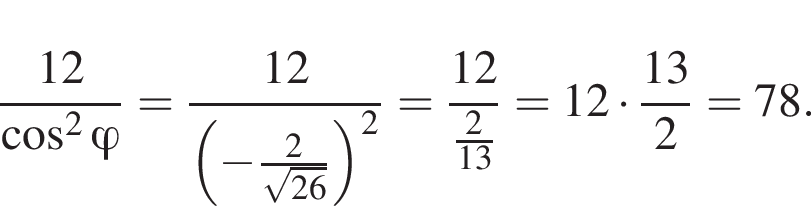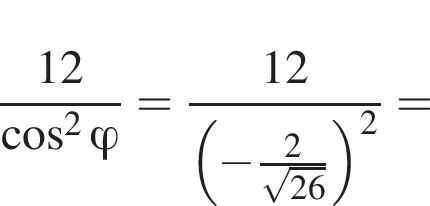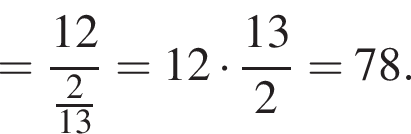На рисунках 1 и 2 изображены правильная треугольная призма ABCA1B1C1 и ее развертка. Найдите площадь боковой поверхности призмы, если длина ломаной ACA1 равна 
и точки A, C, A1 лежат на одной прямой (см. рис. 2).
Среди дробей 
укажите ту, которая равна дроби 
Даны пары значений переменных x и y: (3; 9); (−15; 3); (0; 12); (14; −2); (6; 6). Укажите пару, которая НЕ является решением уравнения x + y = 12.
Используя рисунок, определите верное утверждение и укажите его номер.
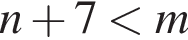
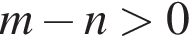
На координатной прямой отмечены точки В(−2), А(6), X(а). Найдите длину отрезка ВХ, если точки В и X симметричны относительно точки А.
В магазин поступило 43 коробки с маслом по 110 пачек масла в каждой. Какое наименьшее количество пачек масла необходимо продавать ежедневно, чтобы масло было распродано не более чем за 60 дней?
На рисунке a || b, 
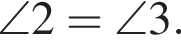Найдите градусную меру угла 4.
Из точки A к окружности с центром O проведены две касательные AB и AC, где B и C — точки касания. Через точки C и O проведена прямая, которая пересекает касательную AB в точке M (см. рис.). Найдите градусную меру угла 1, если ∠AMC = 44°.
Значение выражения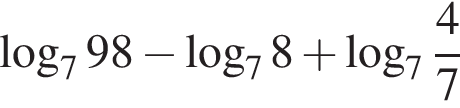 
равно:
Найдите наибольшее натуральное двузначное число, которое при делении на 11 дает в остатке 7.
На координатной плоскости даны точки A(−5; 1) и D(−5; −4). Точка С симметрична точке А относительно оси ординат, а точка В симметрична точке D относительно начала координат. Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Длина большей диагонали четырехугольника ABCD равна ...
Б) Длина наибольшей стороны четырехугольника ABCD равна ...
B) Площадь четырехугольника ABCD равна ...
1) 30
2) 50
3) 
4) 40
5) 
6) 
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
В прямоугольном треугольнике ABC ∠C = 90°, CH — высота, проведенная к гипотенузе,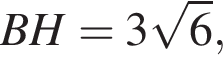 
∠BCH = 30°. Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Длина стороны ВС треугольника АВС равна ...
Б) Длина стороны АС треугольника АВС равна ...
B) Расстояние от точки пересечения биссектрис треугольника ABC
до стороны AB равно ...
1) 
2) 
3) 
4) 
5) 
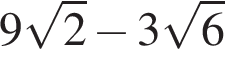
6)
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Дана треугольная пирамида SABC. Точки К и N являются серединами ребер SA и АС соответственно, точка М лежит на прямой SB (см. рис.). Выберите три верных утверждения.
1. Прямая KN параллельна плоскости BSC.
2. Прямая NM пересекает плоскость BSC.
3. Прямая КМ пересекает прямую ВС.
4. Прямая КМ лежит в плоскости ASВ.
5. Прямая NM пересекает прямую ВС.
6. Прямая KN пересекает плоскость BSC.
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 135.
По углам прямоугольной пластины с периметром 448 см вырезали четыре одинаковых квадрата (см. рис.) с длиной стороны, равной 12 см. Края полученной заготовки загнули по линиям 1−4 и получили коробку в форме прямоугольного параллелепипеда объемом 48 дм3. Найдите площадь прямоугольной пластины (в дм2).
Найдите значение выражения
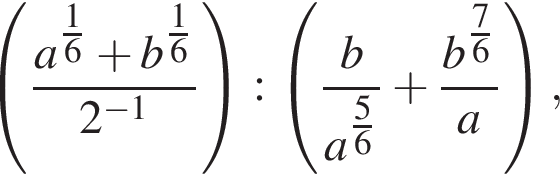
если a = 75 и b = 10.
ABCD — прямоугольник. Точка N — середина стороны ВС. Отрезок DN пересекает диагональ АС в точке О (см. рис.). Найдите площадь четырехугольника ONBA, если площадь прямоугольника ABCD равна 492.
Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К так, что ВК = 2, СК = 3. Найдите значение выражения S2, где S — площадь параллелограмма ABCD, если величина угла А равна 60°.
Найдите наименьшее целое решение неравенства
АС — общая гипотенуза прямоугольных треугольников ABC и ADC. Плоскости этих треугольников взаимно перпендикулярны. Найдите квадрат длины отрезка BD, если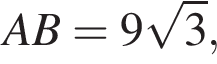 
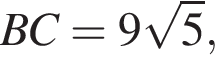AD = DC.
О натуральных числах а и b известно, что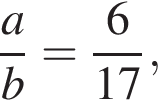 
НОД(a; b) = 4. Найдите НОК(a + b; 10).
В параллелограмме длина одной из сторон вдвое больше длины другой, а острый угол равен 60°. Большая сторона параллелограмма лежит в плоскости α, а его большая диагональ образует с этой плоскостью угол, синус которого равен 
Найдите значение выражения 
где β — угол между плоскостью параллелограмма и плоскостью α.
Прямая, проходящая через вершину К треугольника KMN, делит его медиану MA в отношении 8 : 3, считая от вершины M, и пересекает сторону MN в точке B. Найдите площадь треугольника KMN, если площадь треугольника KMB равна 16.
Отрезок BD является биссектрисой треугольника АВС, в котором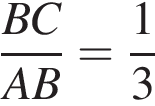 
и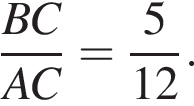 
По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 14 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?
Основанием пирамиды SABCD является выпуклый четырехугольник ABCD, диагонали АС и BD которого перпендикулярны и пересекаются в точке O, АО = 9, ОС = 16, ВО = OD = 12. Вершина S пирамиды SABCD удалена на расстояние 
от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 10 · V, где V — объем большей из частей.
Найдите суму всех целых решений неравенства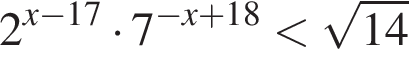 
на промежутке (−25; 25).
ABCA1B1C1 — правильная треугольная призма, все ребра которой равны 3. Точки P и K — середины ребер BC и CC1 соответственно, M ∈ AA1, AM : AA1 = 1 : 3 (см. рис.). Найдите увеличенный в 25 раз квадрат длины отрезка, по которому плоскость, проходящая через точки M, K, P, пересекает грань AA1B1B.
Найдите (в градусах) наименьший корень уравнения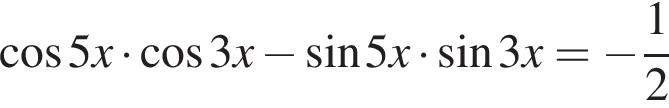 
на промежутке (−80°; 0°).
Найдите произведение наибольшего целого решения на количество всех натуральных решений неравенства 
Две снегоочистительные машины, работая одновременно, очистили всю улицу за 24 мин. Если бы половину улицы очистила первая машина, а затем оставшуюся часть улицы — вторая машина, то вся улица была бы очищена за 50 мин. За какое время (в минутах) вторая машина, работая одна, очистила бы всю улицу, если известно, что она работает медленнее, чем первая машина?
ABCDA1B1C1D1 — куб. Точка K лежит на ребре AB куба так, что AK : KB = 2 : 1. Найдите значение выражения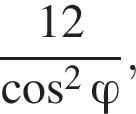 
где φ — угол между прямыми A1K и B1D1.
Из точки А проведем перпендикуляр AH к прямой CB и перпендикуляр AH1 к продолжению отрезка A1A Точка H делит сторону CB равностороннего треугольника ABC пополам, так как является высотой и медианой. Сторона треугольника ABC равна A1C1, треугольники ABC и A1B1C1 равны. Прямоугольные треугольники AA1H1 и ACH подобны по двум углам. Примем длину стороны треугольника ABC за x, x > 0, составим уравнение:
Примем за a сторону AA1 прямоугольника AA1C1C, a > 0. По теореме Пифагора в треугольнике AA1C:
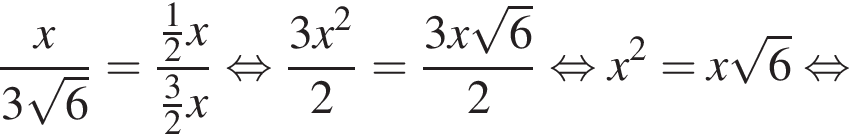
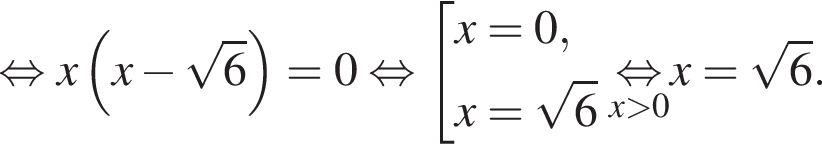
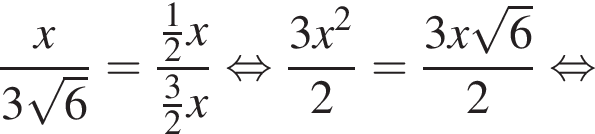
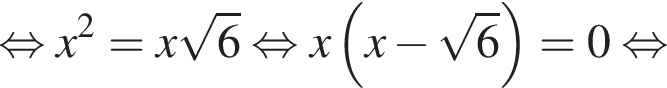
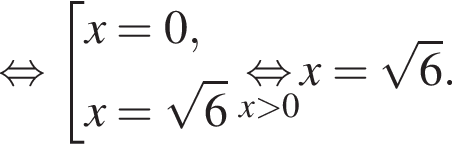
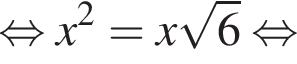
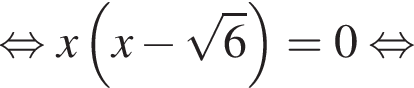
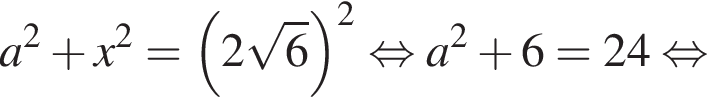
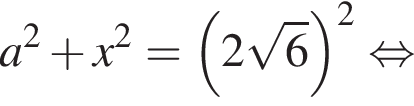
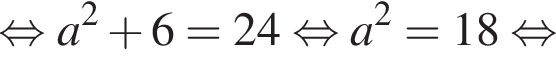
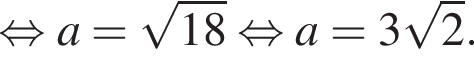
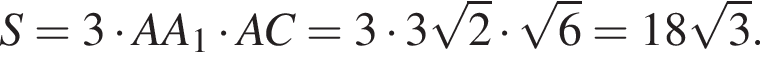
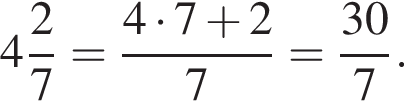
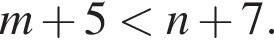
Тогда длина BX равна 
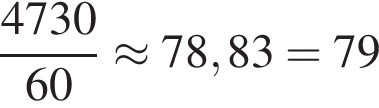пачек масла.
Значит,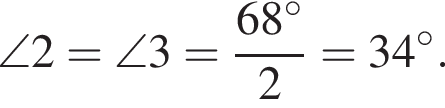 
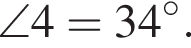
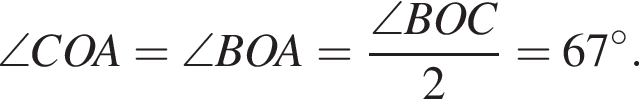
Тогда 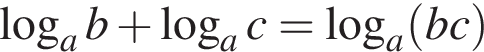и 
и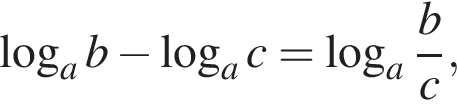 
получаем: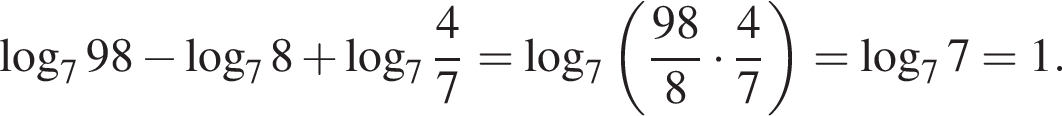
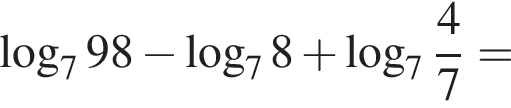
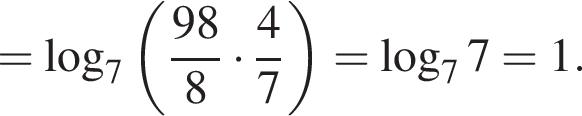
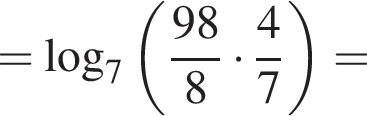
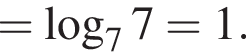
Так как нужно найти наибольшее натуральное двузначное число, то a < 100. Решим неравенство: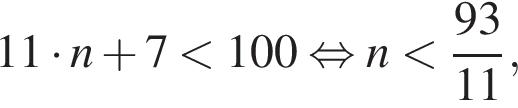
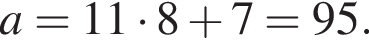
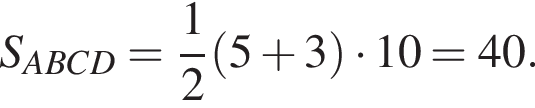
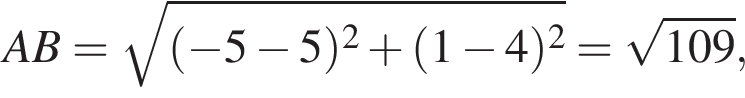
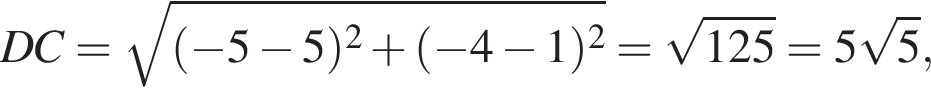
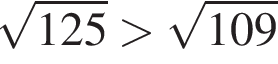и тем более 
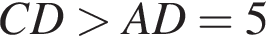и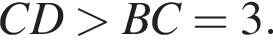 
Значит, наибольшая боковая сторона имеет длину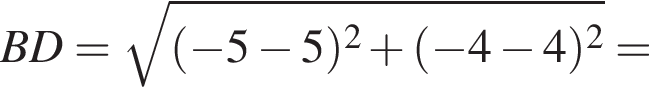 
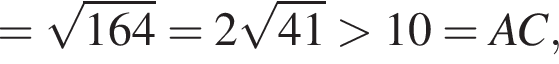
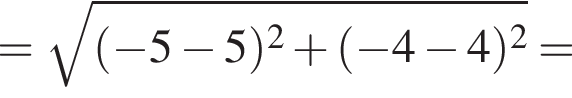
и 
Из прямоугольного треугольника CBA получаем 
и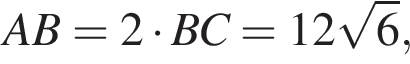 
следовательно,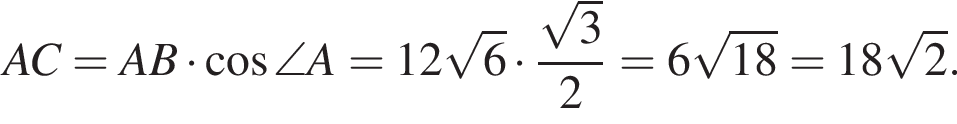 
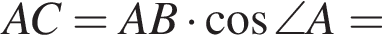
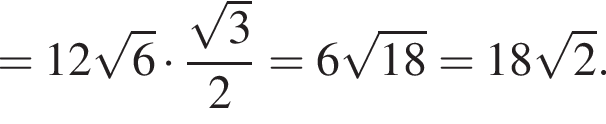
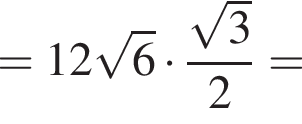
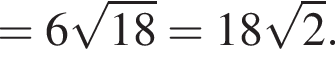
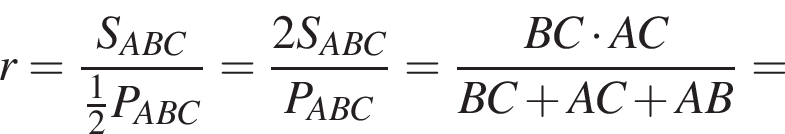
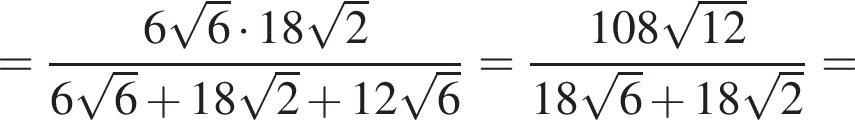
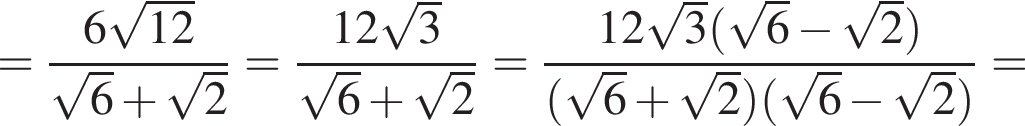
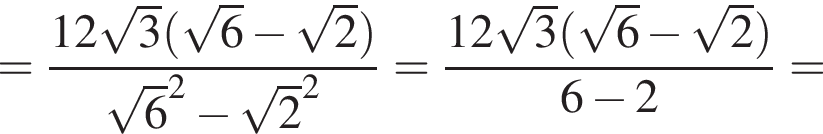
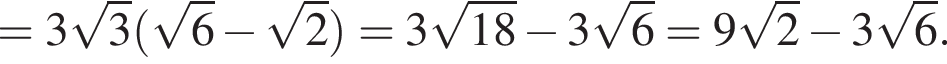
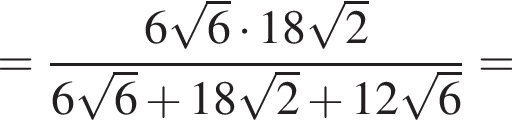
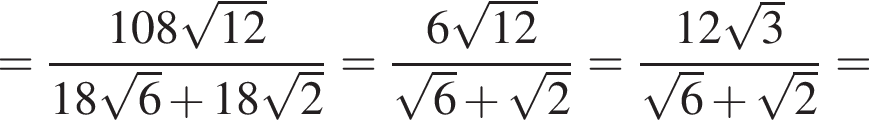
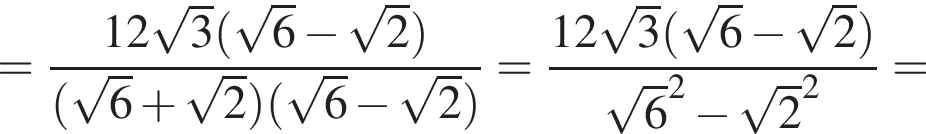
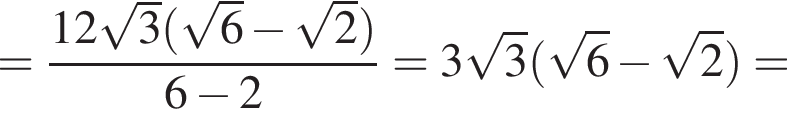
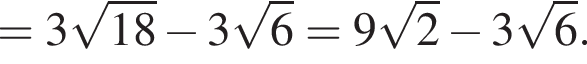
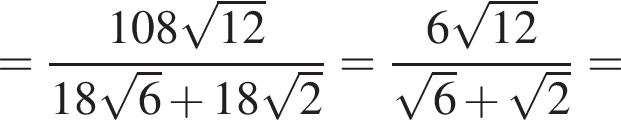
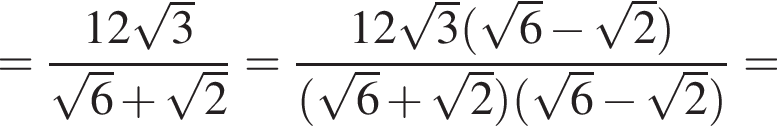
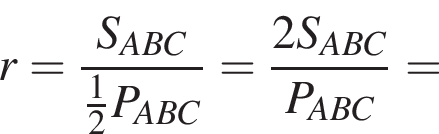
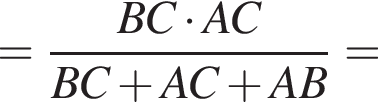
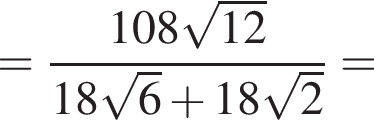
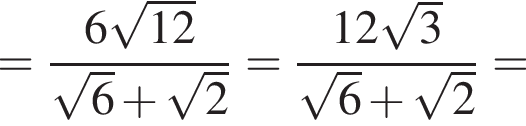
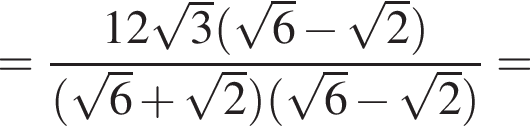
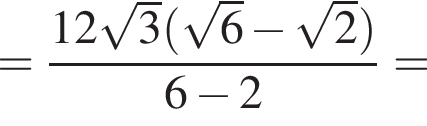
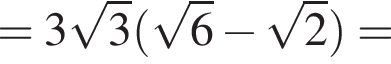
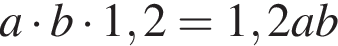кубических дециметра, откуда 
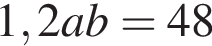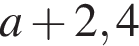и 
и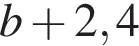 
дециметра, поэтому периметр ее был равен 
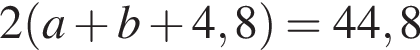дециметра, откуда 
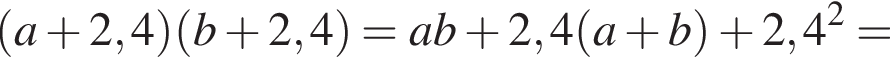
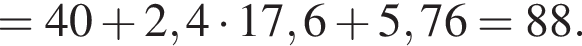
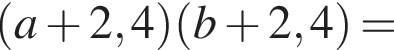
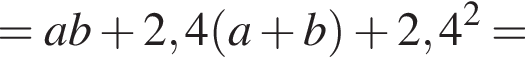
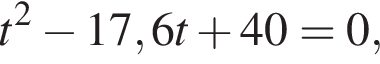поэтому равны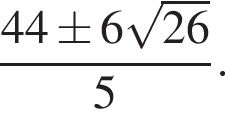 
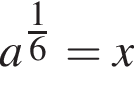и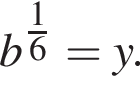 
Тогда получим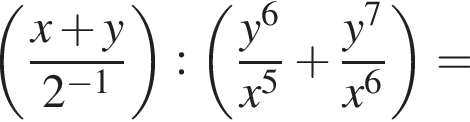 
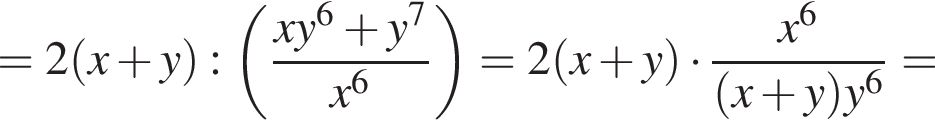
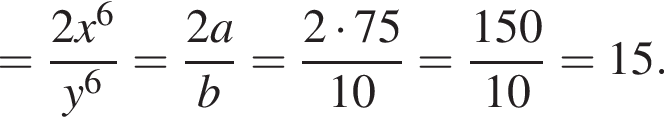
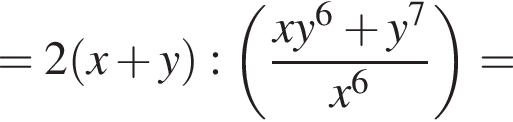
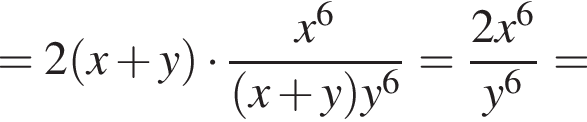
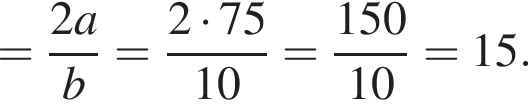
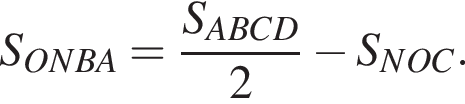Треугольники ONC и AOD подобны по двум углам. Тогда 
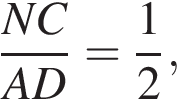отношение площадей подобных треугольников равно квадрату коэффициента подобия, поэтому 
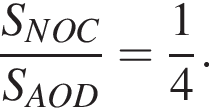Отношение 
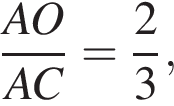тогда 
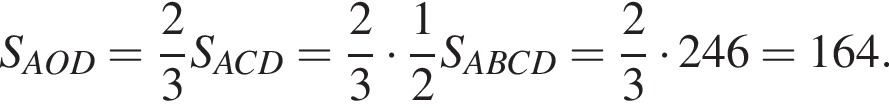
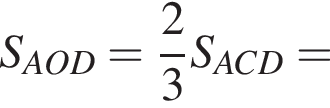
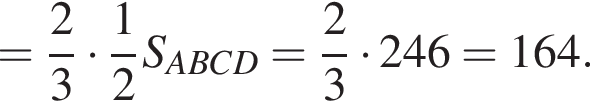
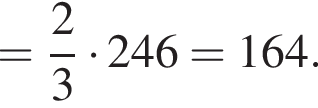
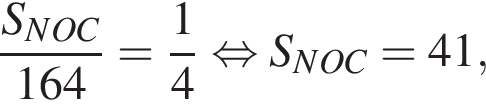то 
где первое равенство равно из-за биссектрисы, второе — накрест лежащие углы. Значит, треугольник ABK равнобедренный и потому AB = 2. Далее,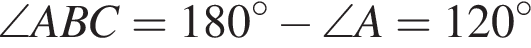 
и потому площадь параллелограмма равна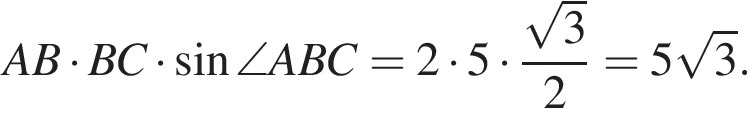 
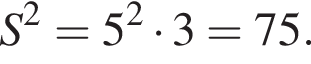
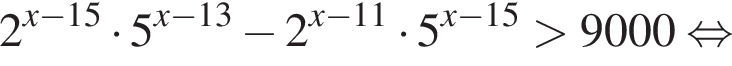
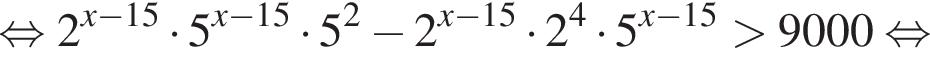
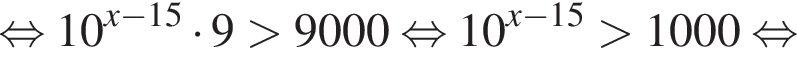
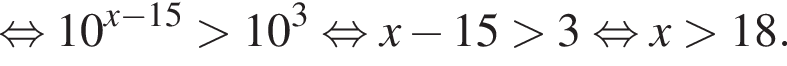
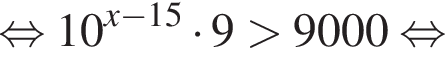
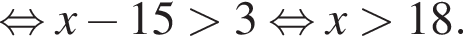
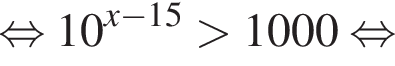
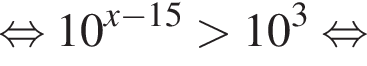
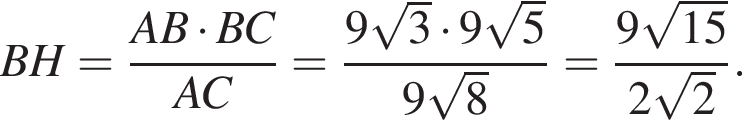
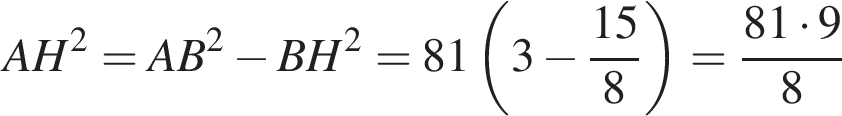
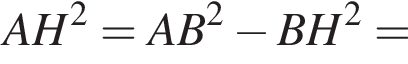
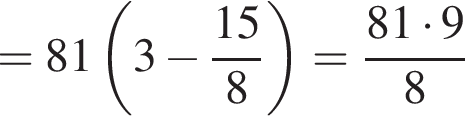
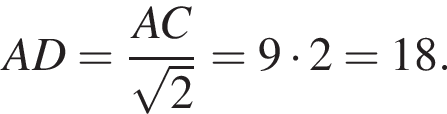
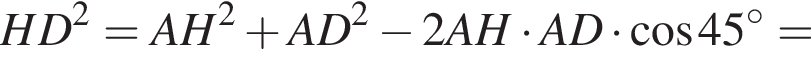
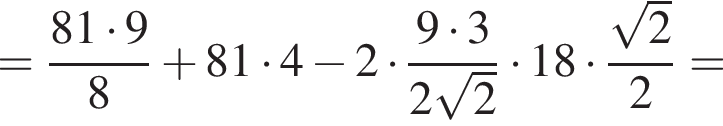
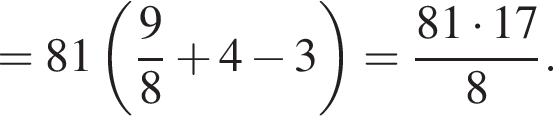
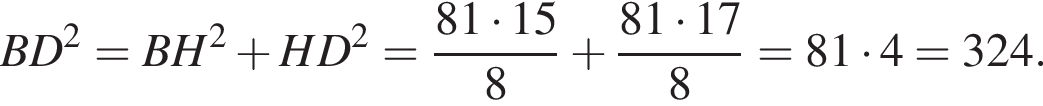
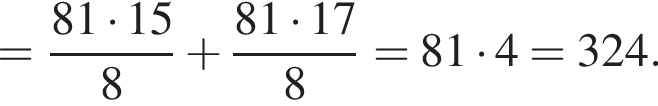
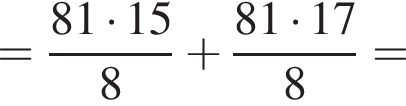
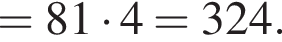
откуда 6b (а значит, и b) кратно 17. Пусть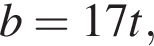 
тогда 
или 
тогда наибольший общий делитель a и b равен t, поскольку 6 и 17 взаимно просты. Значит, t = 4, a = 24, b = 68 и a + b = 92, следовательно, искомое наименьшее общее кратное равно 
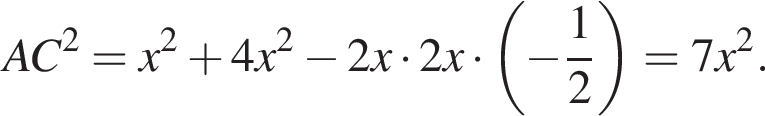
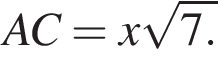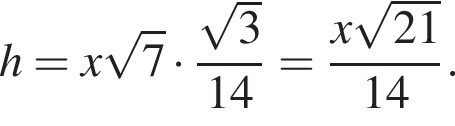
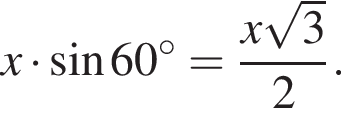Пусть h — расстояние от прямой BC до плоскости α. Тогда 
Тогда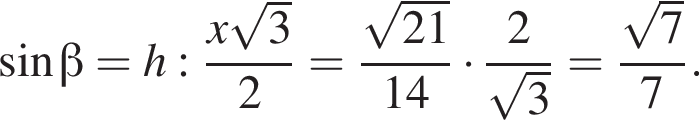 
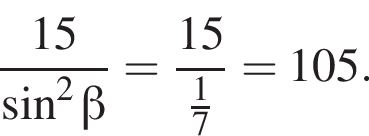
По теореме о пропорциональных отрезках получаем, что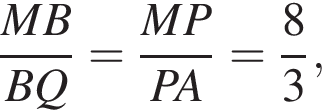 
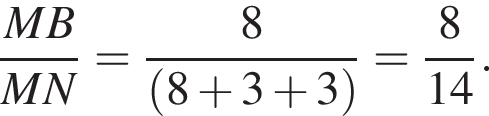
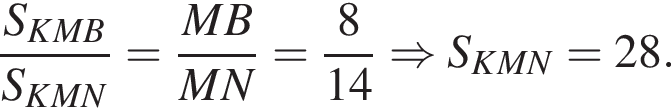
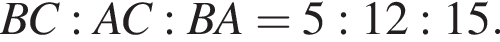По свойству биссектрисы получаем, что 
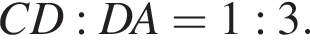Значит, если 
то 
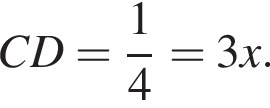
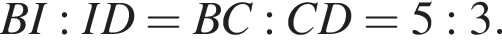Значит, можно считать, что скорость первого тела равна 5υ, а второго 3υ. Время движения обратно пропорционально скорости, из условия следует, что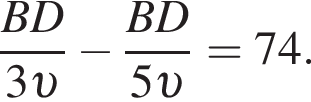 
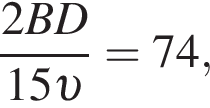откуда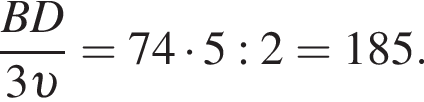 
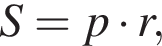где p — полупериметр. Находим: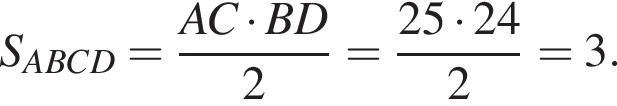
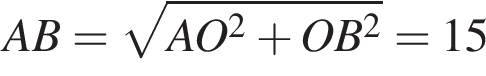и 
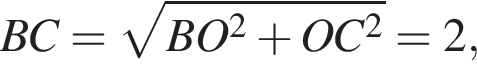следовательно,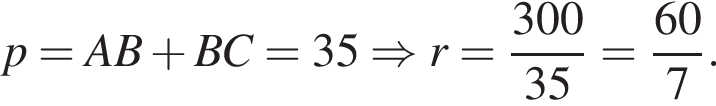 
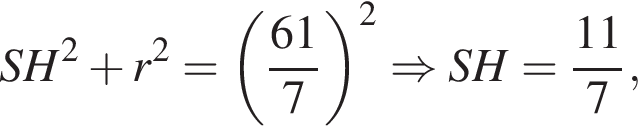
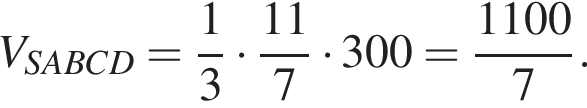
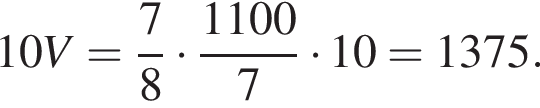
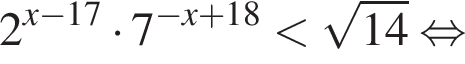
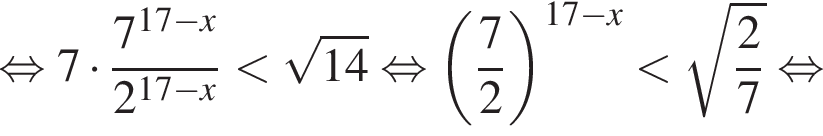
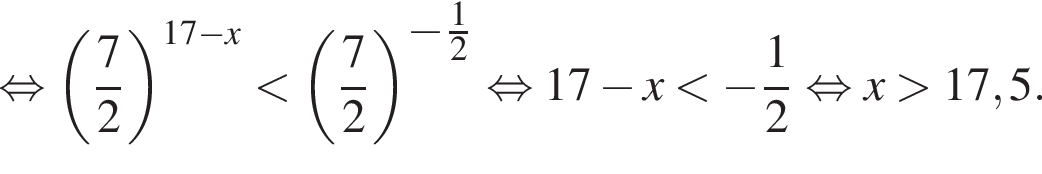
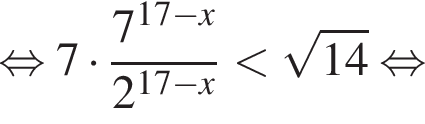
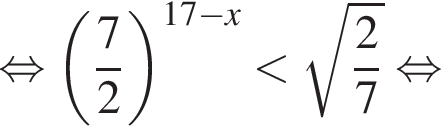
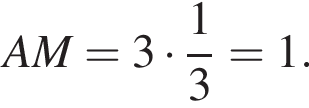и 
от объема исходной пирамиды. Таким образом, 
Треугольники KPC и LBP равны по стороне и двум углам, тогда 
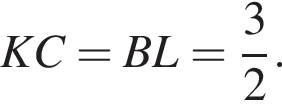Треугольники BQL и AMQ подобны по двум углам, тогда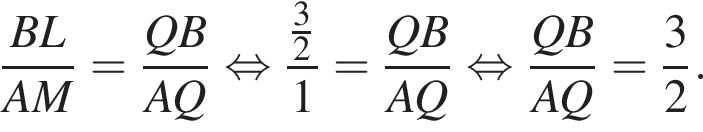
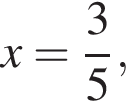
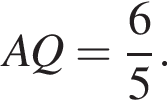По теореме Пифагора: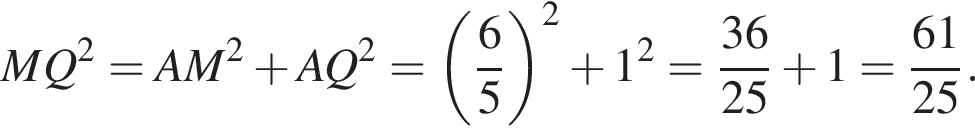
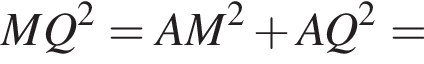
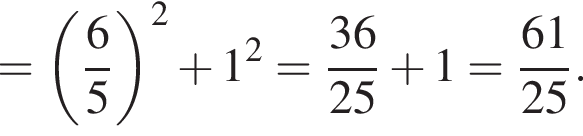
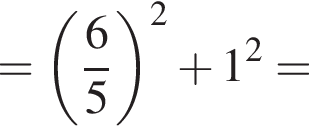
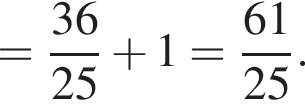
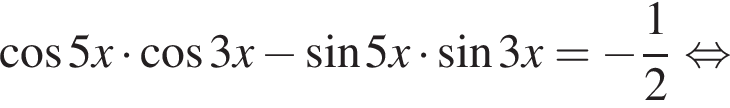
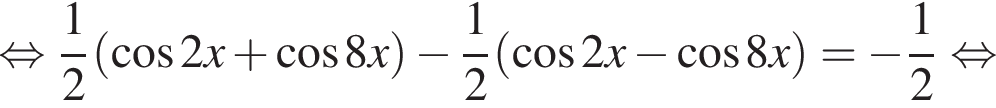
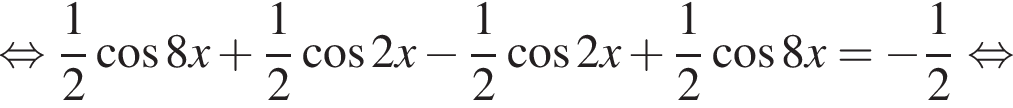
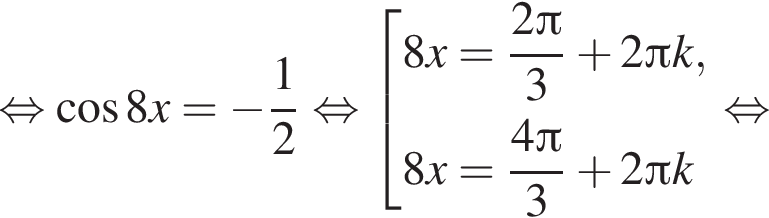
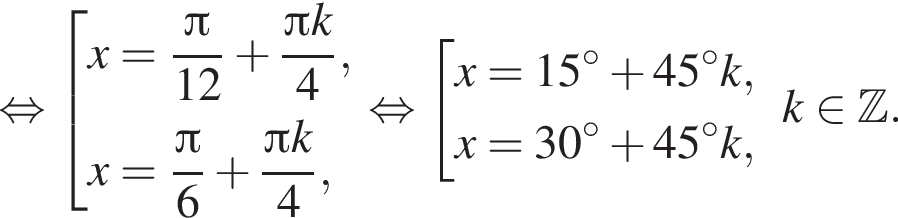
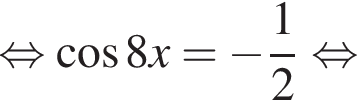
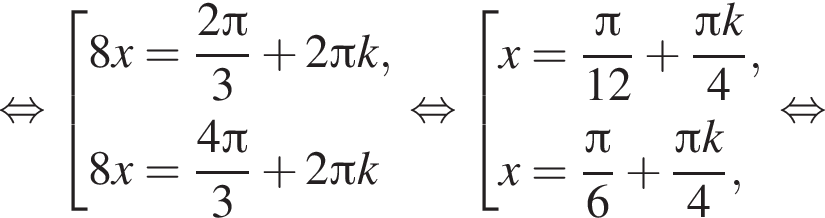
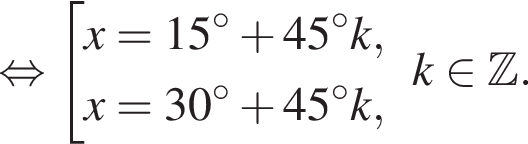
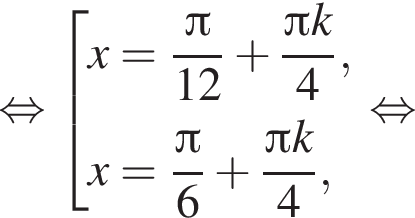
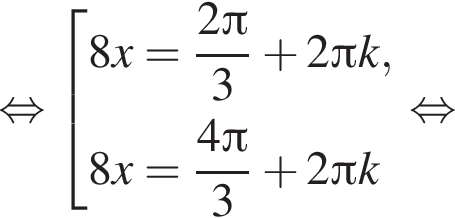
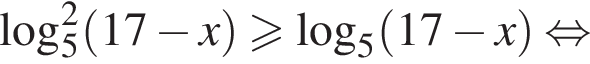
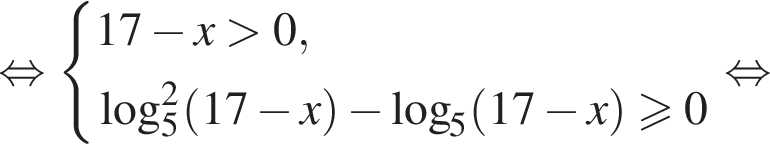
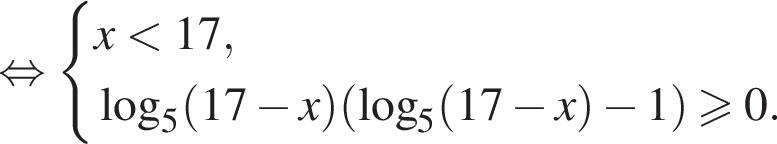
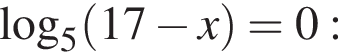
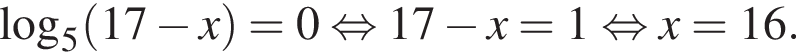
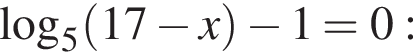
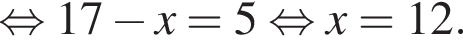
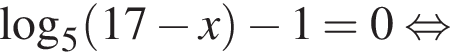
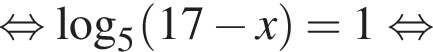
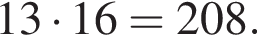
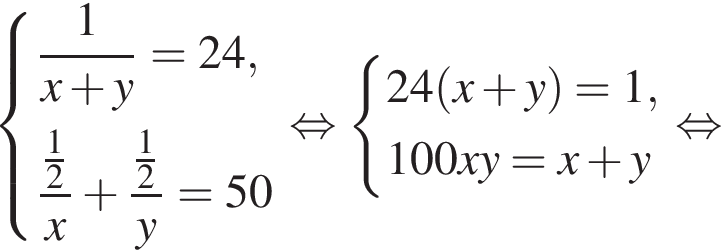
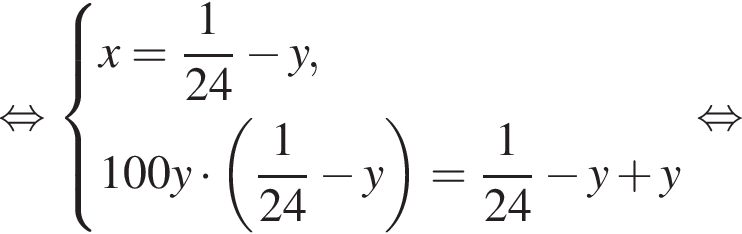
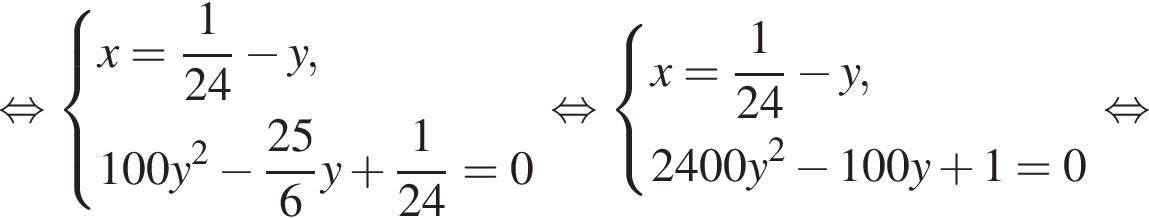
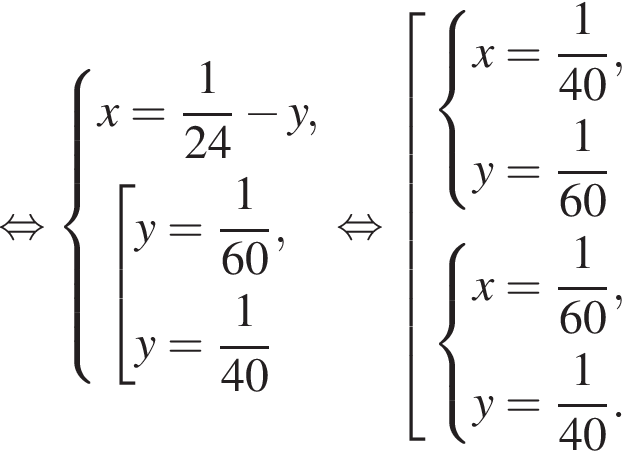
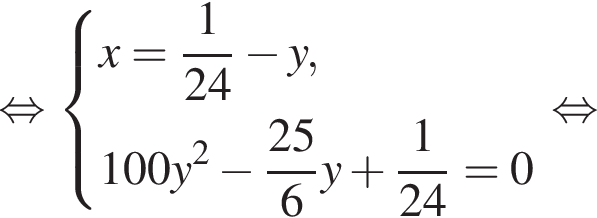
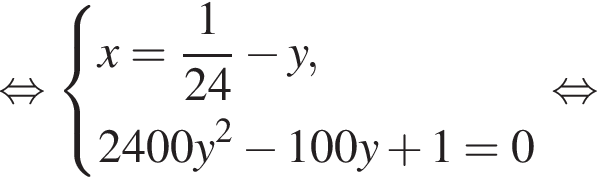
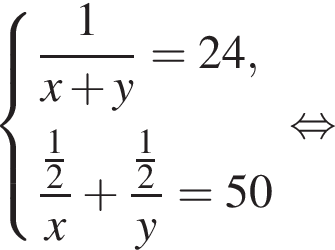
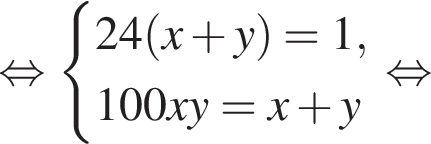
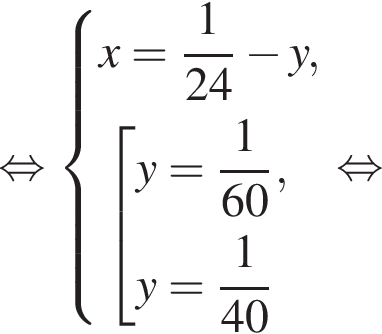
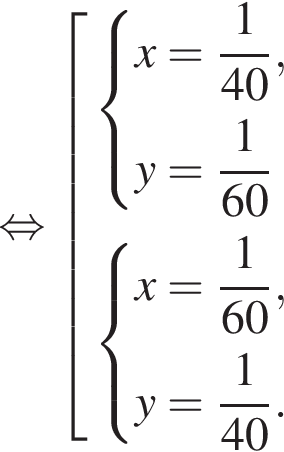
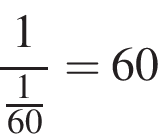а скорость работы второй машины равна 
Вторая машина, работая одна, очистила бы улицу за 
минут.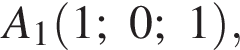
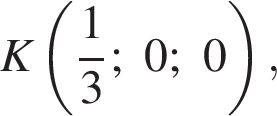
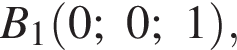
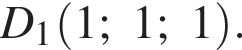Найдем координаты вектора 
и 
